Why Most Stocks are Losers

Erm, Go What?
A colleague sent me a Bloomberg article cheekily entitled, "Everything We've Learned About Modern Economic Theory Is Wrong." The provocateur profiled in the article, a physicist named Ole Peters, attacks one of economists' favorite tools, the expected utility hypothesis, with the claim that the technique mistakenly assumes something called "ergodicity."

That may be. However, what struck me when reading the article was the practical implication for stock market investors: the great power of diversification. The discussion also indirectly explains the cause of the Great Fund Migration, during which investors moved from primarily owning stocks individually, to owning actively managed mutual funds, to owning index funds.

A Winning Proposition?
At the heart of the article is an example: A coin is flipped, delivering a profit if it lands heads and a loss if it lands tails. The profit is 50%, and the loss is 40%.

That bet seems attractive. Those who wager $100 will receive $50 if the coin lands heads and will lose $40 for tails, with each result occurring half the time. That makes the expected return $5, which represents the difference in absolute value between the $50 gain for heads and the $40 loss for tails, divided by the number of equally possible results. To express that gain in stock market terms, with a single coin flip counting one year's worth of equity performance, the investment's expected annual return is 5%.

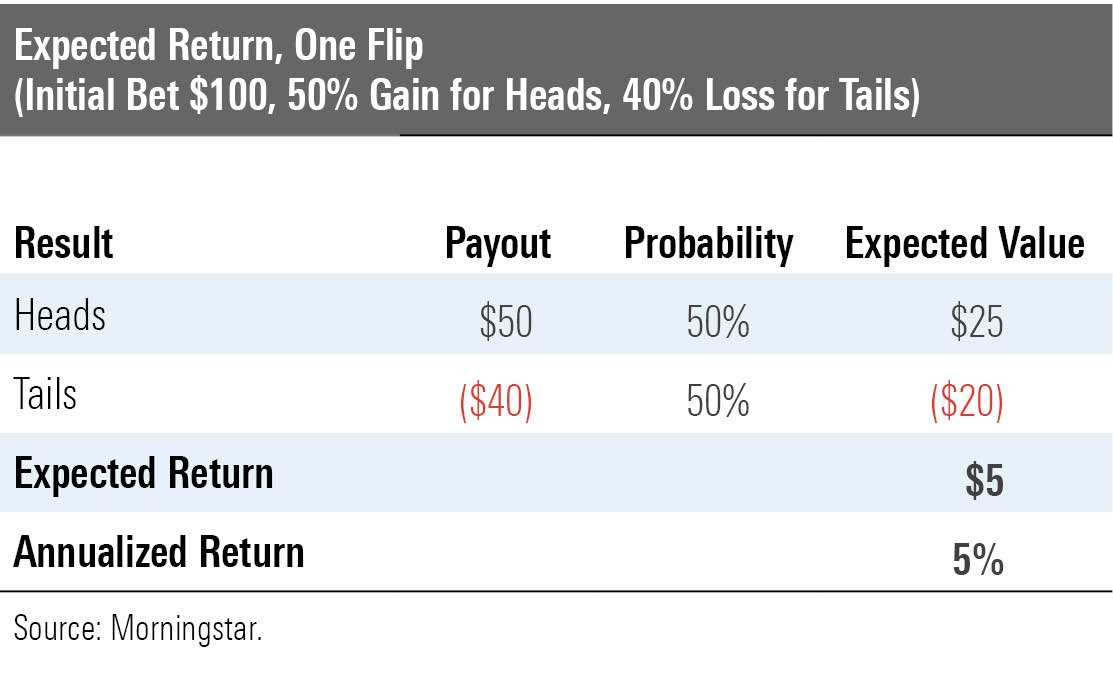
The outlook doesn't change with additional flips. In all cases, the payout for heads exceeds the loss for tails. For example, if the first flip landed heads, then the investor would bet $150 on the second throw, receiving $75 for a result of heads and forfeiting $60 on tails. If, on the other hand, the first flip were tails, then the investor would wager $60, with heads returning $30 and tails costing $24. No matter what its previous sequence, the coin always rewards victories more than it penalizes losses.

The annualized return also remains constant. With two flips, there are four equal possibilities: 1) two heads, 2) heads then tails, 3) tails then heads, and 4) two tails. The table below depicts the payoffs for each outcome, along with that outcome's expected value and the overall expected return. The gain is $10.25, which, on a $100 outlay that was invested for two time periods (that is, coin flips), translates to an expected annualized return of 5%. Nothing changed.

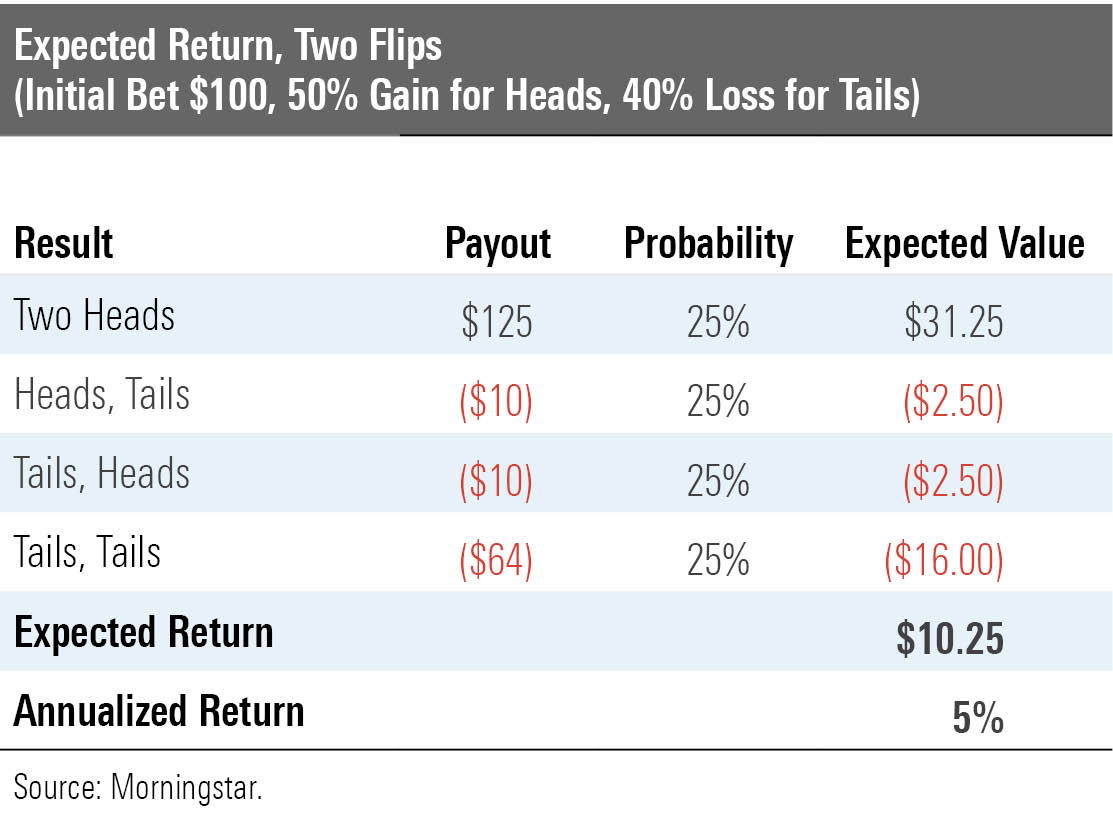
Stuck in the Middle
Note, though, that while half the outcomes in the single-period example were winning, when the wager is extended to two periods that percentage declines. Now, only 25% of the outcomes are profitable. If the coin lands heads both times, it pays $125 on the $100 initial investment--a tidy sum indeed. However, that gain subsidizes the other three possibilities, because both 50/50 combinations lead to a modest decline in wealth, while two straight tails creates a large loss.

This is a strange conclusion. Every possible wager has a positive expected return, yet most participants who bet repeatedly will finish the in red. In addition, the more one plays, the worse the odds become. For two wagers, the median outcome is -10%. Double the investment to four flips, and the median result drops to -19%. Making 10 wagers reduces the median to -41%, 20 to -65%, and 100 to a breathtaking -99.5%. Of such victories disasters are made.

(Note: Although the median result for this series of bets declines rapidly, the percentage of winning bettors does not decrease as quickly and rapidly as implied by the one- and two-coin examples. Thus, for three flips, the percentage of winners once again reaches 50%. The percentage does go down with repetition, but the function is jagged. Also, the numbers change markedly depending upon the size of the bets. The investor’s odds are much better for a series of 40%/30% bets than they are for the 50%/40% proposition, and they are markedly worse yet for 60%/50%.)

Here's why the median erodes. Although each bet faces the same odds, the stakes for the wagers fluctuate, based on the results of the preceding flip. That variation benefits streaks. Wins that follow wins are larger than they otherwise would be, because the investment that is placed at risk has grown. Conversely, losses that succeed losses are less damaging. However, when the flips alternate, the fluctuations become unhelpful, because the wins come after a loss has reduced the stake, while losses come after a win has increased it.

Implications
Fine, you say. How does this concern ergodicity?

Good question. The notion of ergodicity comes from the physical sciences, "relating to a process in which every sequence or sizable sample is equally representative of the whole (as in regard to a statistical parameter." Some believe that in adapting this concept to the field economics, Peters has indeed identified an underlying flaw. Others claim that he has merely reinvented the wheel by disguising existing knowledge with new terminology. In either case, that debate concerns economics, not investments, meaning that I will not (and cannot) address it.

However, I can attest that the coin paradox proves highly instructive about the behavior of the stock market. As with the coin-flip exercise, the expected return for equities is comfortably positive, but those who follow a single betting path--that is, coin-flippers who possess only their own series of results, or equity investors who buy a single stock--will sharply underperform that expectation. In either case, the few winners effectively subsidize the many losers.

This occurs for two interrelated reasons. First, the business world forms a pyramid, with a small number of powerful companies that enjoy growing revenues and high margins resting on the backs of the huddled masses. Second, a company's stock return often oscillates, rising and then falling, falling and then rising. Such behavior erodes principal, as demonstrated by the coin-flip example.

In short, most stocks stink. Fortunately, while those wagering on coin flips must take a single path, equity investors can dramatically improve their odds by buying in bundles--that is, by purchasing stock funds that own dozens or even hundreds of securities, rather than just one. Which, of course, is exactly what they have done. In the 1980s and 1990s, investors switched from mostly buying stocks individually to purchasing actively run funds, and in recent years, they increased their diversification further by indexing. Those decisions were entirely logical.

Of course, it took investors several decades to reach that point--a lag that challenges strong forms of the efficient-market hypothesis. But better late than never.

Einstein vs. Oppenheimer
Speaking of physicists, Albert Einstein allegedly played Robert Oppenheimer in a chess game at Princeton in 1933. The location seems unlikely, because Oppenheimer was then a UC Berkeley professor. But as Oppenheimer regularly taught at Caltech, and Einstein visited in Pasadena in early 1933, they might have played in California.

At any rate, Einstein comes off very well. Oppenheimer's chess abilities, on the other hand, resemble mine. Well, that's one bit of common ground.